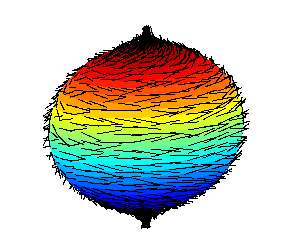
Brace yourselves-because things are about to get hairy.
Imagine a random ball covered in hair. Would you be able to comb it perfectly flat, without any cowlicks or parts? Well, mathematicians say no. The hairy ball theorem isn’t something you would find in your shower drain, it’s a theory that states that a continuous, non- vanishing tangent vector field on an even-dimension does not exist.
In mathematical terms, the “Random ball” is defined as a 2-dimensional sphere. (S²) It’s called a 2D sphere rather than a 3D sphere because all the locations on the surface can be described with two coordinates. Any way you try to assign vectors to each point on a sphere, a discontinuity(part), vector with zero length(bald spot), or a vector that is not tangent to the sphere is bound to exist.
The vanishing point only exists if n in Sⁿ is an even number. If the coordinates of the points on the surface of the shape can be expressed with an odd number of coordinates, like a doughnut (which can be expressed with three coordinates), for example, the hair would be perfectly combable.
This theorem can be applied to global wind circulation. The earth’s winds have magnitude and direction, making it highly comparable to vectors. While the application of the theorem isn’t fully accurate here, since wind blows in a 3D space, wind roughly lives on the surface of the earth, which is a 2D sphere. According to our theorem, there has to be at least one point on earth where the speed of the wind is zero. This can explain the existence of cyclones, anticyclones, and calm points.
The theorem can even be applied to robotics and motion planning. A robot should be able to change its orientations and positions without glitching. When the orientation is derived from a space, the “space” behaves in a sphere-like way. However, according to the hairy ball theorem, directions can not be defined on a sphere completely smoothly. The robot will always have at least one position where a glitch occurs or a change in mode is needed.
It’s quite interesting how a hairy ball can explain phenomena in wind circulation and robotics. Unfortunately, it can not explain that bald spot on your head. That’s just the “vectors” not existing on that spot rather than being undefined.
By. Seojin Yun
Works Cited
https://www.scientificamerican.com/article/maths-hairy-ball-theorem-has-surprising-implications/